潜伏期(incubation period)和再生时间(generation time)是传染性疾病研究中的关键指标，对描述传染病特征和政策制定起着至关重要的作用。为了克服学术界之前的研究问题，周晓华团队借助于更新过程的理论，考察被某删失事件（离开武汉）截断的潜伏期。把潜伏期（从感染到产生症状）看作发生间隔时间(inter-arrival)，离开武汉的感染者居民潜伏期被离开武汉这一事件所截断，再考虑到部分居民可能在离开武汉时（机场、火车站等场所）发生交叉感染，因而可以把离开武汉到产生症状的时间看作是区间删失的前进时间（截断事件到产生症状，forward time）与发生间隔时间（感染到产生症状）这二者的混合，同时考虑了由报告时间引起的区间删失问题。

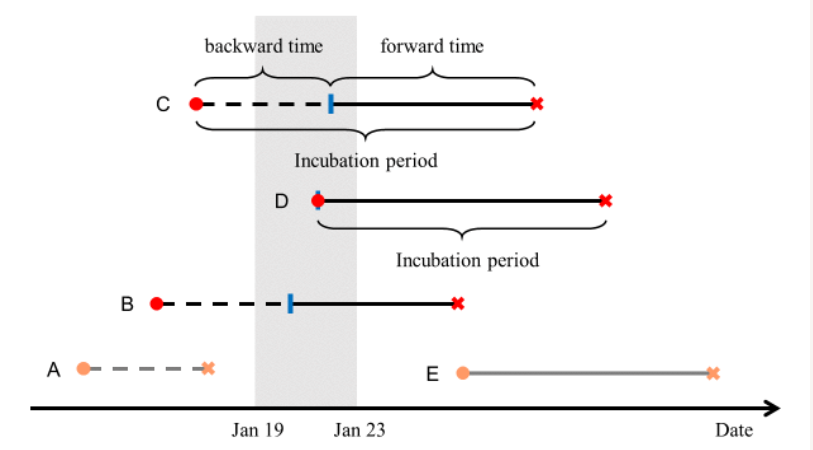
图：潜伏期、后退时间、前进时间。黑色线条表示纳入研究队列的人群，灰色线条表示未纳入研究队列的人群；

实线表示观测到的，虚线表示未观测到的时间段。红色圆：感染时间；红色叉：产生症状时间；蓝色柱：离开武汉时间。

假设潜伏期服从伽马分布、威布尔分布或对数正态分布，观测队列为离开武汉后发病的人群，队列中在离开武汉当天感染的概率（混合概率）为π。在适当的条件下，作者证明了潜伏期分布参数、混合概率的可识别性的数学性质，并证明了这些参数估计量的大样本性质（服从渐进正态分布或截断正态分布）。对于混合概率π的假设检验问题，可以利用似然比检验给出。

和传统的流行病学调查相比，研究团队提出的方法可以减少回忆偏倚，增大可用样本量，有效利用删失信息，为新传染病流行的潜伏期估计提供了一种分析框架，其优势在传染病并爆发初期尤为明显。另外，基于潜伏期和观测到的序列间隔，在适当的假设下，通过反卷积运算，对潜伏期有传染性的疾病提出了再生时间的一个非参数的相合估计。

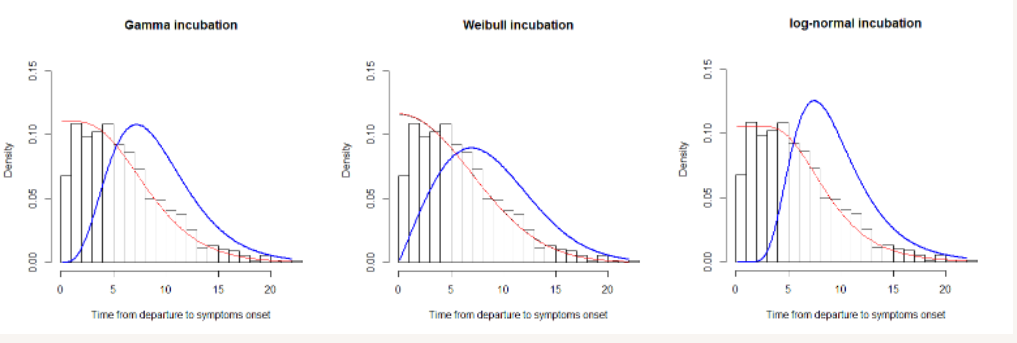
图：潜伏期分布的估计。红线表示前进时间的拟合，蓝线表示潜伏期分布的拟合

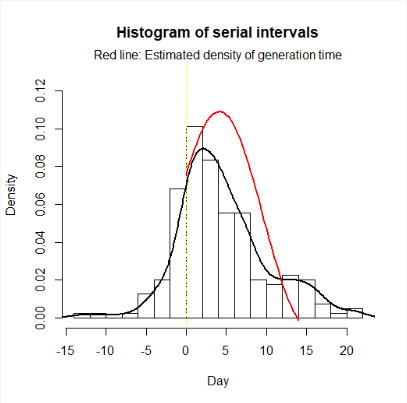
图：再生时间分布的估计。柱状图是序列间隔数据，黑线是序列间隔的非参数拟合，红线是再生时间分布的估计